
Weisstein, Eric W., "Archimedes' Spiral" from MathWorld.Let $r(\theta)=a+b\theta$ the equation of the Archimedean spiral. "Spiral Plate Method for Bacterial Determination". "Adding Color and the Reliability of DLP". "Fluid compressing device having coaxial spiral members". Princeton, New Jersey: Princeton Universoty Press. Nonplussed! Mathematical Proof of Implausible Ideas. ^ "successive turnings of the Archimedean spiral have a constant separation distance" Havil, Julian (2007). And it's also used to model the pattern that occurs in a roll of paper or tape of constant thickness wrapped around a cylinder. They have the appearance of a coil of rope or. Also, Archimedean spirals are used in food microbiology to quantify bacterial concentration through a spiral platter. Polar graphs of the form r at + b where a is positive and b is nonnegative are called Spirals of Archimedes. Archimedean spirals are also used in digital light processing (DLP) projection systems to minimize the "rainbow effect", making it look as if multiple colors are displayed at the same time, when in reality red, green, and blue are being cycled extremely quickly. Asking for a patient to draw an Archimedean spiral is a way of quantifying human tremor this information helps in diagnosing neurological diseases. The coils of watch balance springs and the grooves of very early gramophone records form Archimedean spirals, making the grooves evenly spaced and maximizing the amount of music that could be fit onto the record (although this was later changed to allow better sound quality). Scroll compressors, made from two interleaved Archimedean spirals of the same size, are used for compressing liquids and gases.
The Archimedean spiral has a variety of real-world applications. One method of squaring the circle, by relaxing the strict limitations on the use of straightedge and compass in ancient Greek geometric proofs, makes use of an Archimedean spiral. Many dynamic spirals (such as the Parker spiral of the solar wind, or the pattern made by a Catherine's wheel) are Archimedean. Virtually all static spirals appearing in nature are logarithmic spirals, not Archimedean ones. Other spirals falling into this group include the hyperbolic spiral, Fermat's spiral, and the lituus. 225 bc) to square the circle and trisect an angle. The normal Archimedean spiral occurs when x = 1. equation In spiral Although Greek mathematician Archimedes did not discover the spiral that bears his name ( see figure), he did employ it in his On Spirals ( c. Sometimes the term Archimedean spiral is used for the more general group of spirals There is a curve slightly different from the Archimedean spiral, the involute of a circle, whose turns have constant separation distance in the latter sense of parallel curves.

The constant distances in the Archimedean spiral are measured along rays from the origin which do not cross the curve at right angles, whereas a distance between parallel curves is measured orthogonally to both curves. Some sources describe the Archimedean spiral as a spiral with a "constant separation distance" between successive turns. Taking the mirror image of this arm across the y-axis will yield the other arm. Only one arm is shown on the accompanying graph. The two arms are smoothly connected at the origin. The Archimedean spiral has the property that any ray from the origin intersects successive turnings of the spiral in points with a constant separation distance. The Archimedean spiral has two arms, one for θ > 0 and one for θ < 0. In contrast to this, in a logarithmic spiral these distances, as well as the distances of the intersection points measured from the origin, form a geometric progression. Spiral radius (r): An archimedean spiral with 3 turnings.

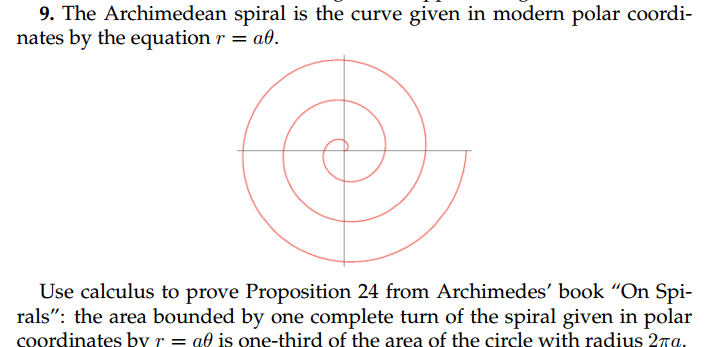
The Archimedean spiral has the property that any ray from the origin intersects successive turnings of the spiral in points with a constant separation distance (equal to 2πb if θ is measured in radians), hence the name "arithmetic spiral". Changing the parameter a will turn the spiral, while b controls the distance between successive turnings.Įxamples: Archimedes Spiral (Mathematica, PolarPlot )Īrchimedes described such a spiral in his book On Spirals. Equivalently, in polar coordinates (r, θ) it can be described by the equation It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity. The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd century BC Greek mathematician Archimedes.


 0 kommentar(er)
0 kommentar(er)
